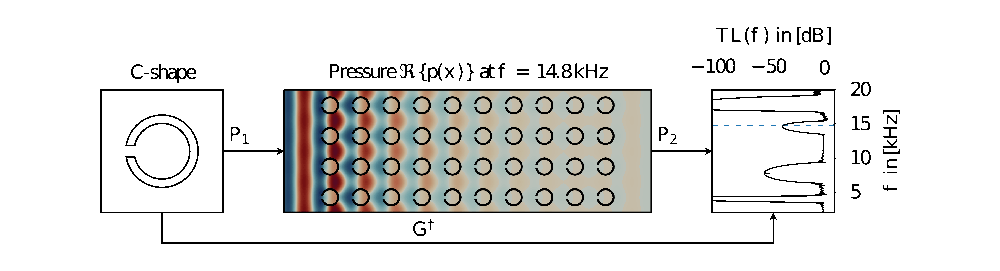
Neural Operators as Fast Surrogate Models for the Transmission Loss of Parameterized Sonic Crystals, NeurIPS 2024, D3S3 Workshop

This collaboration of the Chair of Vibroacoustics of Vehicles and Machines at TUM with my team is part of our investigation of the use of deep learning to accelerate physical simulations.

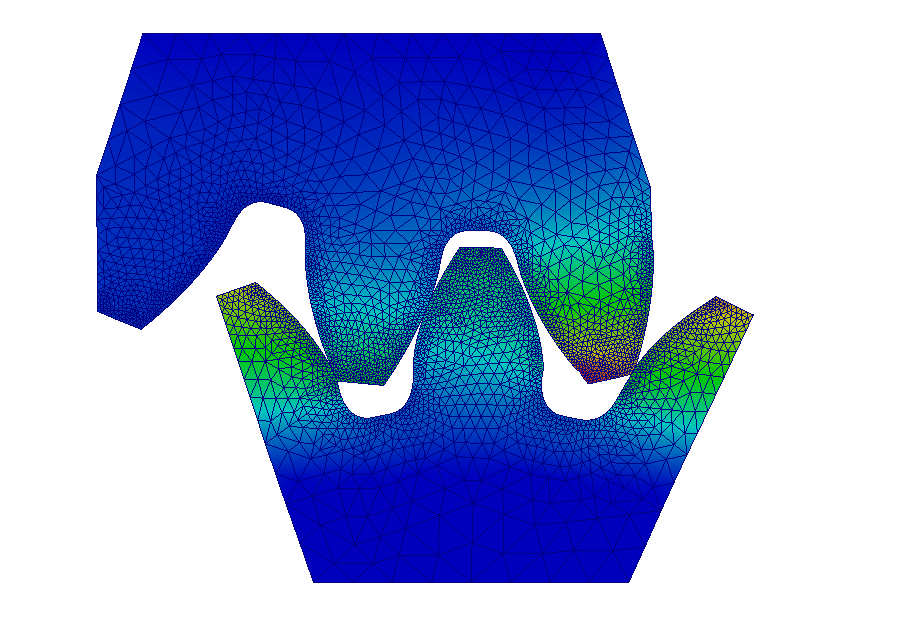
Neural operators serve as efficient, data-driven surrogate models for complex physical and engineering problems. In this work, we demonstrate that neural operators can directly learn the key properties of sonic crystals, a type of acoustic metamaterial consisting of a lattice of parameterized shapes. We predict the transmission loss curve, a critical characteristic in applications, bypassing the expensive meshing and solving steps typical of classical techniques. We evaluate established architectures (DeepONet, FNO) alongside two new ones (DNO, DCO), which demonstrate significant performance improvements. In our experiments, all models achieve high accuracy, while being up to 10⁶ times faster than traditional methods, significantly advancing practical real-time metamaterial design.

All experiments were run by Jakob Elias Wagner, with the support of Johannes D. Schmid, and Samuel Burbulla, the lead developer of continuiti, our library for neural operator learning used for the experiments. The paper was accepted in the NeurIPS 2024 Workshop on Data-driven and Differentiable Simulations, Surrogates, and Solvers.

[Re] Classwise-Shapley values for data valuation (TMLR)

This is the second published paper reproduction in data valuation from my team, as part of our effort to help practitioners apply new methods appearing in the literature. It's one step closer to our goal of a consistent benchmark of data valuation methods.

We evaluate CS-Shapley, a data valuation method introduced in Schoch et al. (2022) for classification problems. We repeat the experiments in the paper, including two additional methods, the Least Core (Yan & Procaccia, 2021) and Data Banzhaf (Wang & Jia, 2023), a comparison not found in the literature. We include more conservative error estimates and additional metrics, like rank stability, and a variance-corrected version of Weighted Accuracy Drop, originally introduced in Schoch et al. (2022). We conclude that while CS-Shapley helps in the scenarios it was originally tested in, in particular for the detection of corrupted labels, it is outperformed by the conceptually simpler Data Banzhaf in the task of detecting highly influential points. For the reproduction we built upon and extended pyDVL.

All experiments were run by Markus Semmler. The paper appeared in Transactions of Machine Learning Research (TMLR 2024) and was accepted for the 2023 edition of the Machine Learning Reproducibility Challenge (MLRC 2023).

[Re] If you like Shapley then you'll love the core (MLRC2022)

This was the first of many paper reproductions to come out of the TransferLab, as part of our effort to help practitioners apply new methods appearing in the literature.

We investigate the results of Yan and Procaccia's If you like Shapley then you'll love the core in the field of data valuation. We repeat their experiments and conclude that the (Monte Carlo) Least Core is sensitive to important characteristics of the ML problem of interest, making it difficult to apply, despite superior performance in some settings. For the reproduction we built upon and extended pyDVL.

All experiments were run by my esteemed colleague Anes Benmerzoug. The paper appeared in the 2022 edition of the Machine Learning Reproducibility Challenge (MLRC 2022).

Class-wise and reduced calibration (ICMLA 2022)

Probabilistic classifiers' confidence vectors should ideally mirror true probabilities, but most common models don't achieve this, making methods to measure and improve calibration vital. This is not straightforward for multi-class problems. We suggest two techniques. First, a reduced calibration method simplifies the original problem, and we prove that solving this reduces miscalibration in the full problem, allowing the application of non-parametric recalibration methods that otherwise fail in high dimensions. Secondly, we present class-wise calibration methods, derived from 'neural collapse' phenomena and the notion that most accurate classifiers are unions of different functions, each calibratable separately per class. These generally outperform non-class-wise methods, especially with imbalanced data sets. Combining the methods leads to class-wise reduced calibration algorithms, reducing prediction and per-class calibration errors. We validate our methods on real and synthetic datasets and provide all code as open source here.

This is joint work with my great colleagues Anes Benmerzoug and Michael Panchenko, appearing at the 21st International Conference on Machine Learning and Applications (ICMLA 2022).

PaperWhy

PaperWhy was my attempt to contribute to the sisyphean endeavour not to drown in the immense Machine Learning literature. With thousands of papers every month, keeping up with and making sense of recent research has become almost impossible. By routinely reviewing and reporting about papers I helped myself and hopefully someone else.

Since establishing the TransferLab in 2022, this work continues in the form of paper pills.

Bayesian model selection

In this note we introduce linear regression with basis functions in order to apply Bayesian model selection. The goal is to incorporate Occam's razor through Bayesian analysis in order to automatically pick the model optimally able to explain the data without overfitting. This is joint fun with Philipp Wacker.

Monte Carlo Tree Search

MCTS is a moderately recent (2006) algorithm for playing games by partially building their decision trees. The key is to use random simulations of the game for those choices which seem most fruitful according to a criterion balancing exploration of new venues and exploitation of good ones. An implementation in Python for a simple game of Quantum TicTacToe provides a nice testbed. This is joint fun with Ana Cañizares, based on work by Philipp Wacker.

K - nearest neighbours

KNN is one of the simplest non-parametric classification algorithms. In this note, we start from basic ideas in kernel density estimation and using Bayes' rule we derive this simple (albeit slow and sloppy) algorithm which "only" requires the computation and sorting of distances in $L^p$. We test its performance on the CIFAR10 dataset with a C++11 implementation using Armadillo and a viewer written with Qt for the results.

K-means and Gaussian Mixtures

K-means is a simple clustering algorithm which matches each data point to exactly one of $K$ clusters in a way such that the sum of the squares of the distances of each data point to the center of mass of its assigned cluster is minimal. We review how this minimization can be performed iteratively in a manner closely linked to Expectation Maximization for Gaussian mixtures. We also briefly discuss K-Means++.

Expectation maximization

EM is a generic iterative algorithm for the maximization of the log likelihood. Following (very closely) Bishop's classical book we discuss its general form, applied to Gaussian models with latent variables as motivation. Some limitations are discussed. Finally we also say a few words about the Kullback-Leibler divergence and other information theoretic ideas to show why EM works.

Support Vector Machines

Starting with some elementary ideas on how to tackle the task of assigning labels to images, we progress onto the classical Perceptron, then introduce Optimal Margin Classifiers and finally the primal version of the SVM. From there we do a short detour through dual Lagrange methods and introduce the standard dual formulation of the SVM and the construction of higher dimensional feature spaces with the kernel trick. Along the way we discuss optimisation methods which enable us to use SVMs on large data sets. We provide an implementation written in C++11, using Armadillo and Qt.

Data assimilation

DA is the task of incorporating data into models given by stochastic dynamical systems. In the simpler discrete case, one considers stochastic dynamics given by $v_{j + 1} = Ψ (v_j) + ξ_j,$ with i.i.d additive noise, together with a sequence of observations given by $y_{j + 1} = h(v_{j + 1}) + η_{j + 1}$, where $η_j$ is again i.i.d. These are Python implementations of a few algorithms and examples from Law & Stuart's book Data Assimilation, partly written in collaboration with Philipp Wacker.

Hidden Markov Models

A (pure, vectorized) Python implementation of an HMM with discrete emissions given either by probability tables or Poisson distributions. Parameter estimation is done using the Baum-Welch algorithm for HMMs, which actually is Expectation Maximization. In this application we experience how badly EM tends to get stuck in local optima. This code was written during a short stay at the chair of Computational Neuroscience in the department of Neurobiology of the Ludwig-Maximilians-Universität München.

Adaptive Rejection Sampling

ARS is a general technique for sampling from a log-concave distribution. An upper bound of the target density is computed using tangents to its logarithm, then transformed back into a sum of exponentials from which it is easy to sample. After explaining the algorithm we provide basic theoretical justification for it. In a simple Python implementation we also test autograd, a package for Automatic Differentiation. Work with Álvaro Tejero.

SML @ CMU

Python + Cython implementation of some algorithms from Larry Wasserman's course "Statistical Machine Learning" at Carnegie Mellon University. For now, I only have nonparametric regression, with Nadaraya-Watson, Local Polynomial Regression and Generalized or Leave-One-Out cross-validation applied to select the bandwidth. For the multidimensional case I implemented standard Backfitting for Additive Models and SpAM (Sparse Additive Models) for the high dimensional case.

A hierarchy of multilayered plate models (ESAIM: COCV)

We derive a hierarchy of plate theories for heterogeneous multilayers from three dimensional nonlinear elasticity by means of Γ-convergence. We allow for layers composed of different materials whose constitutive assumptions may vary significantly in the small film direction and which also may have a (small) pre-stress. By computing the Γ-limits in the energy regimes in which the scaling of the pre-stress is non-trivial, we arrive at linearised Kirchhoff, von Kármán, and fully linear plate theories, respectively, which contain an additional spontaneous curvature tensor. The effective (homogenised) elastic constants of the plates will turn out to be given in terms of the moments of the pointwise elastic constants of the materials.

Energy Minimising Configurations of Pre-strained Multilayers (J. Elast.)

We investigate energetically optimal configurations of thin structures with a pre-strain. Depending on the strength of the pre-strain we consider a whole hierarchy of effective plate theories with a spontaneous curvature term, ranging from linearised Kirchhoff to von Kármán to linearised von Kármán theories. While explicit formulae are available in the linearised regimes, the von Kármán theory turns out to be critical and a phase transition from cylindrical (as in linearised Kirchhoff) to spherical or saddle-shaped (as in linearised von Kármán) configurations is observed there. We analyse this behaviour with the help of a whole family ($I^{θ})_{θ∈(0,∞)}$ of effective von Kármán functionals which interpolates between the two linearised regimes. We rigorously show convergence to the respective explicit minimisers in the asymptotic regimes $θ → 0$ and $θ → ∞$. Numerical experiments are performed for general $θ∈(0,∞)$ which indicate a stark transition in a critical region of parameters θ.

Effective theories for multilayered plates (Ph.D. thesis)

We derive by $Γ$-convergence a family of effective plate theories for multilayered materials with internal misfit for scaling laws ranging from Kirchhoff's theory to linearised von Kármán. The main addition is the central role played by an intermediate von Kármán-like theory, where a new parameter interpolates between the adjacent regimes. We also prove the $Γ$-convergence of this limiting regime to the other two as well as the relevant compactness results and we characterise some minimising configurations for the scalings considered. Finally, we numerically investigate the interpolating regime employing the open source toolkit FEniCS to implement a discrete gradient flow. This provides empirical evidence for the existence of a critical value of the parameter around which minimisers are of different nature. We show $Γ$-convergence of the discretisation and compactness as the mesh size goes to zero.

Some remarks on the contact set for the Signorini problem (Opusc. Math.)

We study some properties of the coincidence set for the boundary Signorini problem, improving previous work in the literature. Among other new results, we show here that the convexity assumption on the domain made previously in the literature on the location of the coincidence set can be avoided under suitable alternative conditions on the data.

On the contact between two linearly elastic bodies (Master's thesis)

We first introduce the problem of the contact of two elastic bodies in the context of classical linear elasticity, then gather all necessary results for the proof of existence and uniqueness of a solution. The main proof of existence is conducted using two different approaches, depending on the coercivity of the bilinear form associated with the elastic potential. We briefly present a finite element discretization and an algorithm for the solution. In particular we focus on some fairly recent advances in the resolution of the non-linearity at the contact zone via iterative methods using a mortar method with dual Lagrange multipliers.

On a contact problem in elasticity (Bachelor's thesis)

After a quick review of linear elasticity theory, we study the classical problem which considers the stationary equilibrium of an elastic body resting on a frictionless surface (Signorini problem). Its essential property is found in the unilateral boundary conditions given in subsets of the boundary unknown a priori which model the lack of knowledge about the region where contact happens and make the problem non-linear. The coincidence set, where the inequalities defining the boundary conditions become equalities, is then studied in both the vectorial and the scalar settings from two viewpoints. (...)

pyDVL: The python data valuation library

pyDVL strives to offer reference implementations of algorithms for data valuation with a common interface compatible with sklearn and a benchmarking suite to compare them. As of version 0.6.1, pyDVL provided robust, parallel implementations of: Leave One Out, Data Shapley values with different sampling strategies, Truncated Monte Carlo Shapley, Exact Data Shapley for KNN, Owen sampling, Group testing Shapley, Least Core, Data Utility Learning, Data Banzhaf Beta Shapley and the influence function. In addition, we provide analyses of the strengths and weaknesses of key methods, as well as detailed examples.

This is joint work with many in the TransferLab team.

Despite its name TeXmacs isn't either a plugin for Emacs nor a frontend to TeX. It defines a document format, features a macro language for extensions, innumerable plugins with embedded sessions, a vector graphics tool, scientific spreadsheets, bibliography management, remote sessions and a long, long list of features. On top of all that TeXmacs provides god-like powers over your documents thanks to Scheme. Try it and never look back!

PzzApp

A simple 15-puzzle game written in Cocoa with Ana Cañizares. This is our first and only application in this language, mostly written during an intense weekend-hackathon. Don't raise your expectations too high.

rubiQ

An OpenGL interface for a Rubik's cube solver. I wrote this after my first algebra course, where we used semi-direct products to model the group of transformations of the cube. The solver used brute-force to compute the movements graph for the last layer of the cube, assuming the first two have been completed. Written in C++ and Qt.

Clong!

A clone of the 1972 classic Pong written in clojure with the idea of having fun and learning clojure while coding it. We use a naive implementation of the Entity-Component-System framework, closely following Chris Granger's blog post Anatomy of a Knockout.